Comparación de medias entre muestras relacionadas
Dos muestras están relacionadas si sus observaciones están asociadas de alguna manera. El caso típico es el de una medición a un grupo de gente (por ejemplo: nivel de glucosa en sangre - muestra 1) y esa misma medición a la misma gente pero luego de algún tiempo o de algún procedimiento ( nivel de glucosa en sangre luego de tomar X medicamento - muestra 2).
Esto es un caso distinto al de muestras independientes en el cual asumimos que no hay relación entre las muestras. En muestras relacionadas usamos también el test T para analizar si la media entre ambas muestras es significativamente distinta o no, pero corrigiendo por el hecho de que las muestras corresponden a mediciones sobre la misma población y por lo tanto, parte de la variablidad es propia de las individuos de la muestra.
Recordemos que el test T asume que las muestras provienen de una población que se distribuye normalmente y que ambas tienen misma varianza. Para corroborar estos supuestos se pueden aplicar ciertos test que se explican con más detalle en “muestras independientes”. Recordemos también que el test T es robusto ante no cumplimiento de los supuestos siempre y cuando no sea una diferencia alevosa. (Distribución con varias modas por ejemplo.)
Antes de comenzas a aplicar en R esta metodología nos parece útil que tengan en mente que el test T de muestras relacionadas no es más que un test T de una sola muestra (donde se analiza si determinada muestra tiene media distinta de X) pero disfrazado. Por qué? Porque básicamente lo que se hace es calcular la diferencia entre ambas muestras relacionadas y aplicar el test T de una muestra a esta nueva variable para determinar si es o no distinta de 0. En caso positivo significa que las muestras tienen media distinta.
Comenzamos generando las variables. Vamos a seguir con el mismo ejemplo del otro post. Salario de quienes estudiaron estadística, antes y después de obtener un título de posgrado.
set.seed(2)
# 1000 individuos con carrera de grado en ámbito de la estadística
Muestra1 <- rnorm(1000, mean = 80000, sd = 7000)
# Los mismos 1000 individuos pero luego de obtener un posgrado
Muestra2 <- Muestra1 + rnorm(1000, mean = 20000, sd = 10000)Como se puede ver desde la generación de las variables, lo que hicimos fue aumentar el salario en $20000 promedio con cierto desvío para todos los individuos. Por lo tanto tenemos dos muestras de los mismos 1000 individuos, antes y después de obtener un posgrado. Como lo generamos nosotros ya sabemos a priori las conclusiones pero con el objetivo de entender nos es útil.
Gráficamos para tener visibilidad sobre la data.
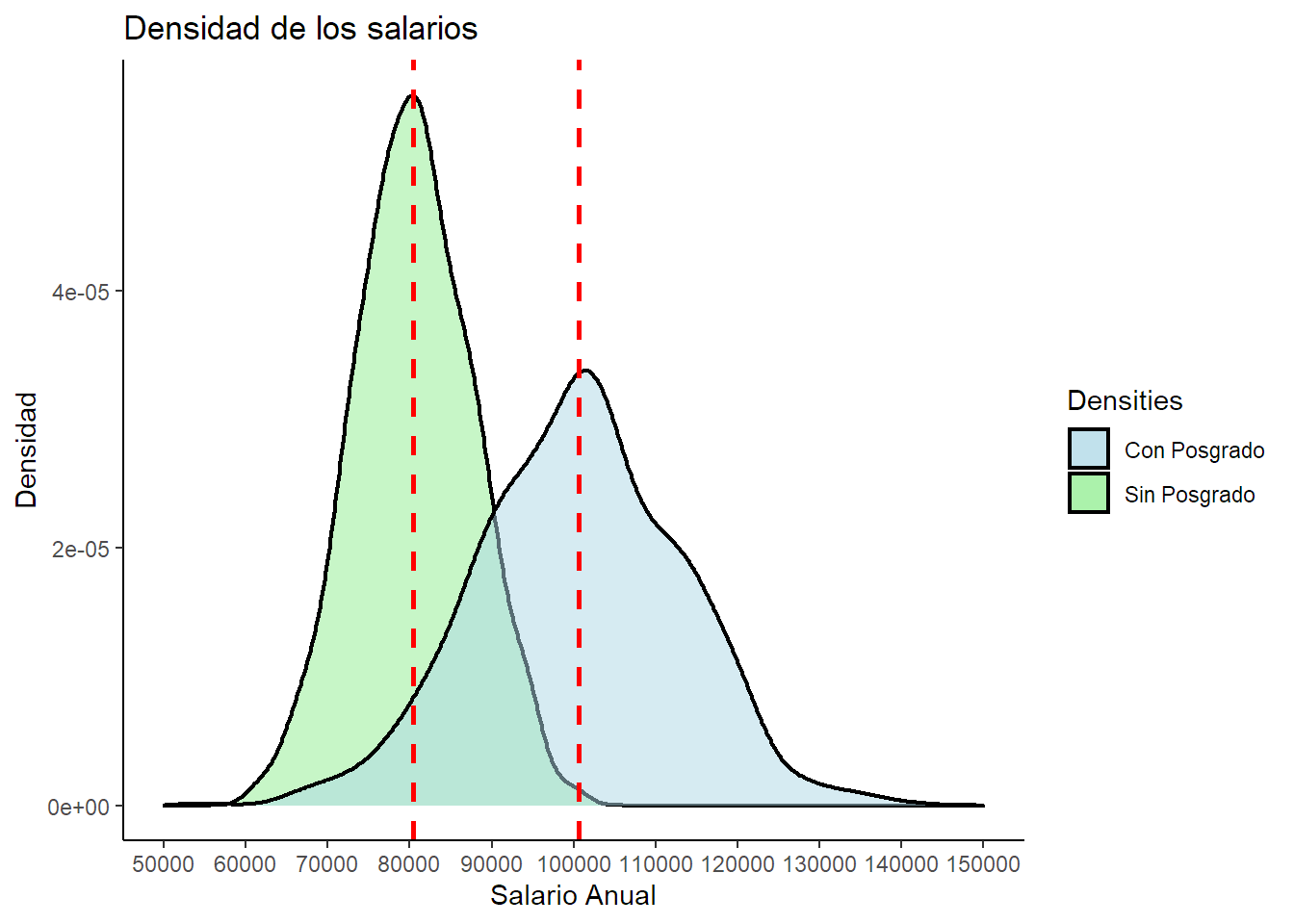
A simple vista vemos que al obtener un posgrado los individuos pasan a tener un salario promedio mayor aunque quizás con un poco mas de varianza alrededor de la media. El test T nos va a permitir determinar si esta diferencia es estadísticamente significativa.
# Paired = TRUE para indicar que son muestras relacinadas.
paired_test <- t.test(Muestra2, Muestra1, paired = TRUE)
paired_test##
## Paired t-test
##
## data: Muestra2 and Muestra1
## t = 64.294, df = 999, p-value < 2.2e-16
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## 19593.34 20827.03
## sample estimates:
## mean of the differences
## 20210.18Como comentamos antes, lo que hace de fondo el test t con la opción paired = TRUE es restar observación tras observación el valor de Muestra1 al de Muestra2 y a esta nueva variable aplicar el test. La hipótesis nula es que la diferencia entre medias es igual a 0 ( - que las medias son iguales -). La nueva variable generada, la resta de entre las variables Muestra1 y Muestra2 es simplemente la diferencia de salario para cada individuo luego de obtner un posgrado. Obviamente hay que estar seguros que las observaciones en ambas muestras corresponden en orden para todos los individuos.
Analizando el output vemos que el estadístico T es 64.294 con 999 grados de libertad, lo que concluye en un p-value muy cercano a 0. Por lo tanto podemos rechazar tranquilos la hipótesis nula con un nivel de significativdad de 0.05. Por otra parte vemos que el promedio de las diferencias es de 20210.18 y el intervalo de confianza al 95% se extiende de 19593.34 a 20827.03.
A modo de conclusión, corroboramos lo que sabíamos por haber generado la data nosotros. Las variables relacionadas Muestra1 y Muestra2 tienen medias distintas.
